論理回路記号一覧表と使い方

論理回路の理解は、エンジニアやプログラマーにとって不可欠なスキルです。しかし、複雑な記号や回路図を正確に理解し、効率的に作成するのは容易ではありません。そこで、論理回路記号を体系的に学ぶことが非常に重要です。

本記事では、論理回路記号の一覧表とその使い方を詳しく解説します。基本的な論理ゲートや複雑な回路まで、各記号の意味と使い方を理解することで論理回路の理解が容易です。さらに、実際に回路図を作成するためのソフトウェア「EdrawMax」についても紹介します。

ドラック&ドロップで論理回路記号をカンタンに使えるEdrawMax

プライバシー保護 | マルウェアなし　

1.  論理回路記号一覧表

論理ゲートを理解するには、その論理回路記号を覚えなくてはいけません。ここでは、基本的な論理ゲートであるANDやORを含めた以下の一覧表の論理記号を解説します。

論理ゲート	論理記号	論理式
AND		Z=A・B
OR		Z=A+B
NOT		Z=A(——) (-)
BUFFER		Z=A
NAND		Z=A・B(——————)
NOR		Z=A+B(——————)
XOR
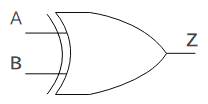XNOR

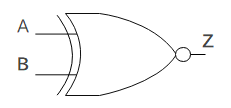ここで取り上げる論理記号はどれも重要な記号なので、繰り返し学習していきましょう。

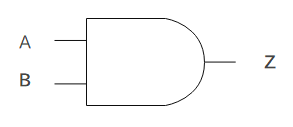
1.1 AND

AND回路は「論理積」とも呼ばれ、2つの入力がどちらも1である時に出力が1である回路です。

論理式は、「Z=A・B」と表されます。

上図はAND回路の回路記号です。真理値表は以下のとおりです。

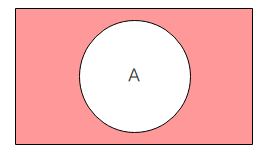
ベン図で表わすと、理解しやすいです。

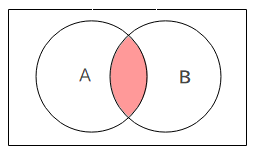
入力がすべて1であるときに出力が1になるのが、AND回路です。

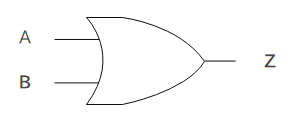
1.2 OR

OR回路は「論理和」とも呼ばれ、2つの入力のどちらか一方が1である時に出力が1である回路です。

論理式は、「Z=A+B」と表されます。

上図はOR回路の回路記号です。真理値表は以下のとおりです。

ベン図で表わすと、以下のとおりです。

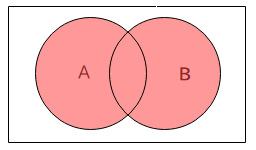
入力のどちらかが1であるときに出力が1になるのが、OR回路です。

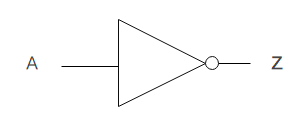
1.3 NOT

NOT回路は否定の意味で、入力と出力を反転します。たとえば、入力が1である時に出力が0である回路です。

論理式は、「Z=A(——」と表されます。

上図はNOT回路の回路記号です。三角の右側にある丸が否定の意味を表します。真理値表は以下のとおりです。

ベン図で表わすと、以下のとおりです。

入力に対して出力が反転するのが、NOT回路です。

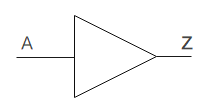
1.4 BUFFER

BUFFERは入力をそのまま出力します。たとえば、入力が1である時に出力が1である回路です。

論理式は、「Z=A」と表されます。上図はBUFFERの回路記号です。真理値表は以下のとおりです。

入力に対してそのまま出力するのが、BUFFERです。

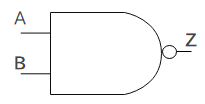
1.5 NAND

NAND回路は「否定論理積」とも呼ばれ、2つの入力がどちらも1である時に出力が0である回路です。

論理式は、「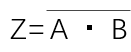」と表されます。

上図はNAND回路の回路記号です。真理値表は以下のとおりです。

入力がすべて1であるときに出力が0になる、AND回路の出力を反転したものがNAND回路です。

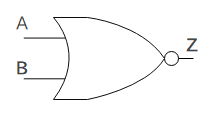
1.6 NOR

NOR回路は「否定論理和」とも呼ばれ、2つの入力のどちらか一方が1である時に出力が0である回路です。

論理式は、「Z=A+B(——————)」と表されます。

上図はNOR回路の回路記号です。真理値表は以下のとおりです。

入力のどちらかが1であるときに出力が0になる、OR回路の出力を反転したものNOR回路です。

1.7 XOR

XOR回路は「排他的論理和」とも呼ばれ、2つの入力が異なる時に出力が1である回路です。

論理式は、「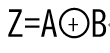」と表されます。

上図はXOR回路の回路記号です。真理値表は以下のとおりです。

異なった入力があるときに出力が1になるのが、XOR回路です。

1.8 XNOR

XNOR回路は「否定排他的論理和」とも呼ばれ、2つの入力が同じ時に出力が1である回路です。

論理式は、「」と表されます。

上図はNXOR回路の回路記号です。真理値表は以下のとおりです。

入力が同じであるときに出力が1になるのが、NXOR回路です。

2.  論理回路記号の使い方

実際にEdrawMaxを使用して論理回路図を作成する手順を紹介します。

2.1 テンプレートを探す

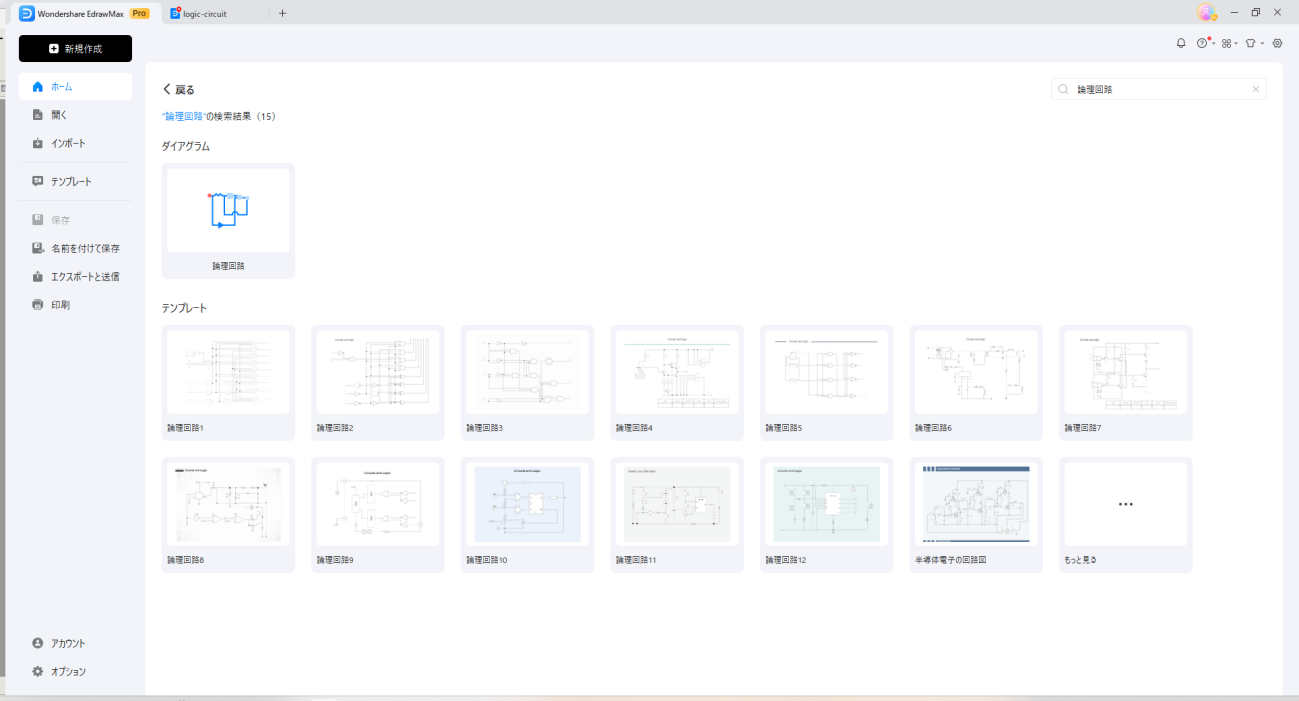
EdrawMaxを起動し、「おすすめ」からテンプレートを探します。すぐに見つからない場合は、検索窓から論理回路図を検索してみましょう。

上図は論理回路を検索した画面です。論理回路のテンプレートが12種類表示されてました。さらにテンプレートを検索する場合は、「もっと見る」をクリックすると、他のユーザが作成したテンプレートを検索できます。

2.2 図形の配置

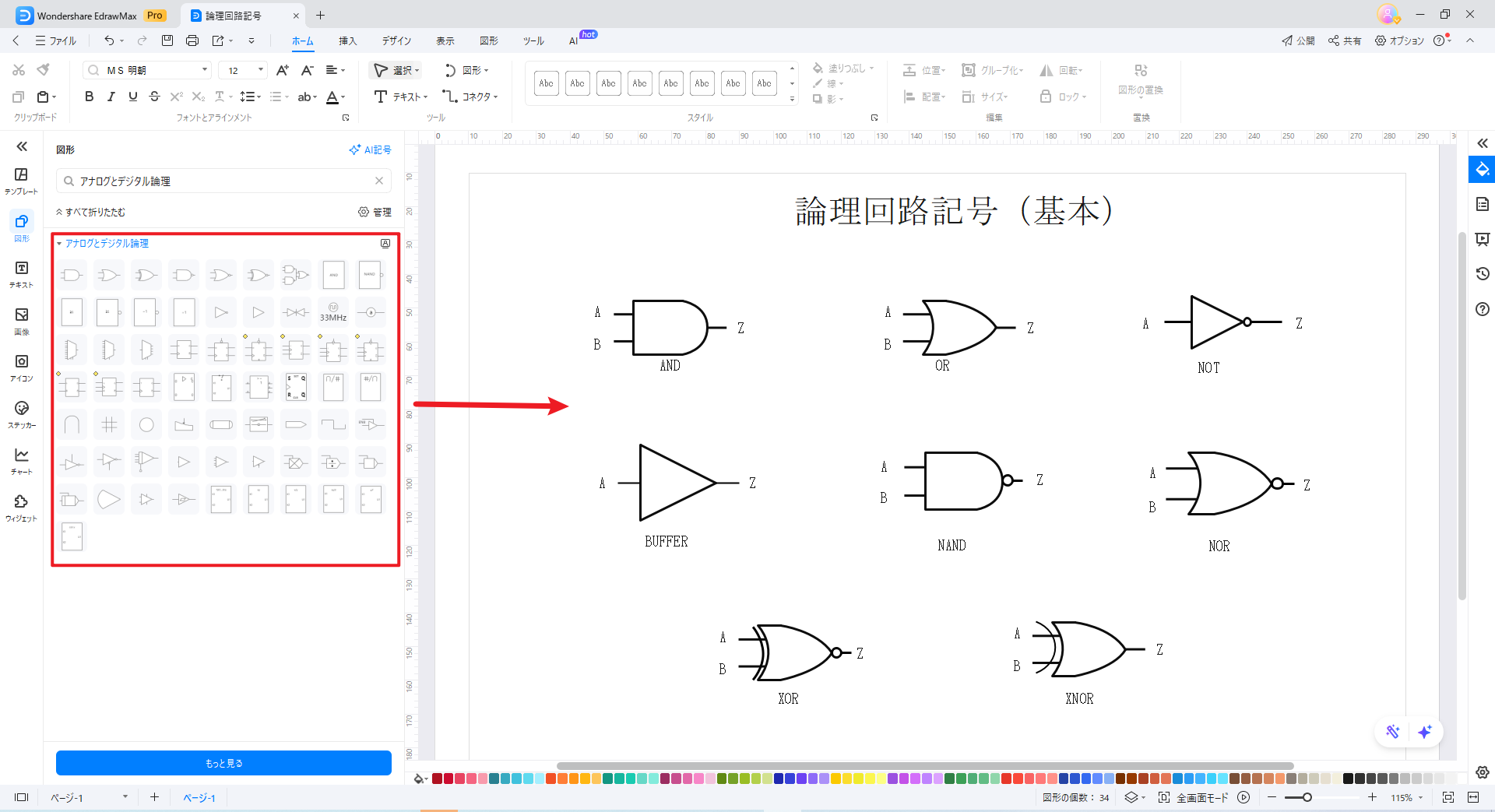
よく使う論理記号が登録されているので、画面左にある図形ライブラリから論理記号を検索します。

ドラッグ＆ドロップで必要な論理回路記号をキャンバス上に配置します。配置した記号はサイズを変更したり回転したり、自由に変更できます。

2.3 接続とカスタマイズ

配置した論理記号を接続し、必要に応じて入力と出力にラベルを付けます。接続線もドラッグ＆ドロップで簡単に引けます。図形の色やサイズを変更し、見やすくカスタマイズします。テキストを追加して、各要素の説明を記入することも可能です。

完成した図面を保存します。PDFや画像ファイルでも保存でき、チームメンバーと共有可能です。

3.  論理回路作成フリーソフト——EdrawMax

論理回路記号を使った図面は「EdrawMax」で作成するのがおすすめです。EdrawMaxは図面作成に特化したソフトウェアで、論理回路を誰でも簡単に作成できます。ここでは、EdrawMaxの基本機能と特徴を解説します。

3.1 EdrawMaxの基本機能

EdrawMaxは、多機能で直感的なインターフェースを持つ図面作成ソフトウェアです。論理回路図作成にも対応でき、以下の基本機能があります。

• ドラッグ＆ドロップ操作
• 豊富なテンプレート
• カスタマイズ可能な図形や記号
• インポート/エクスポート機能

操作に慣れていない方でも簡単に、直感的な操作で簡単に図形を配置・編集できます。さまざまな回路図テンプレートが用意されており、すばやく高品質な図面を作成可能です。論理回路記号を含むシンボルや図形が50,000以上用意され、図形のサイズや色などを自由にカスタマイズできます。多様なファイル形式に対応し、作成したファイルは任意の形式で出力可能です。

3.2 EdrawMaxの特徴

EdrawMaxは、論理回路図の作成において以下の特徴があります。

• 豊富な論理回路記号
• 使いやすいインターフェース
• 自動配置と整列

標準的な論理ゲート（AND、OR、NOTなど）から複雑な回路素子まで、幅広い記号ライブラリを搭載しています。これにより、あらゆる論理回路図を簡単に描けます。使いやすいインターフェースは、初心者からプロフェッショナルまで誰でも簡単に使用可能です。オブジェクトの自動配置や整列機能が充実しており、美しい回路図を迅速に作成できます。

4.  FAQ：mil 記号と論理回路記号の関係

論理回路を表すためにはmil記号を理解しなくてはいけません。Mil記号と論理回路記号はどのような関係があるのかをFAQ形式で解説します。

4.1 mil記号とは？

MIL記号は、論理演算を行う電子回路を図示する記号です。MILは「military（軍事）」の頭文字をとったもので、MIL規格のMIL-STD-806に基づいて定められています。ANDやORなどの論理ゲートを表すために使われます。

記号の形状は、たとえばANDは「D」に似た形をしており、NANDはANDに否定を意味する「○（丸）」が付いています。

4.2 mil記号で論理演算する方法は？

基本情報技術者試験やITパスポート試験でも出題される論理演算です。ここでは、基本情報技術者令和2年試験問22を参考にしてみましょう。

入力A・Bにそれぞれ0と1を入力した4パターンで数字を図上に記入します。AND、OR、NOT記号の入力と出力をそれぞれのパターンで入力すると、以下の図のとおりです。

この結果を真理値表で表します。

該当する選択肢は、（イ）です。

実際に試験で解答する方法は、入力A・Bでどちらも0を計算すると選択肢が（ア）（イ）に絞られます。次に入力Aを0、入力Bを1を計算すると選択肢（イ）を導き出せます。

このように論理演算でAND・OR・NOT回路を組み合わせると、2進数の加算回路を作成できます。加算回路ができるので、組み合わせによって四則演算をすべて計算できます。

5.  まとめ

論理回路記号は、AND、OR、NOTが基本的な論理ゲートです。基本がわかればNORやXORなども理解できます。論理記号を理解することで、論理回路の設計と解析が容易になります。

EdrawMaxは多機能で直感的なインターフェースを持つ図面作成ソフトウェアであり、論理回路図の作成に非常に効果的です。豊富なテンプレートや論理回路記号のライブラリなど多くの特徴を備えているため、誰でも簡単に高品質な回路図を作成できます。

論理回路の設計や学習において、この記事で紹介した知識は非常に役立ちます。今すぐEdrawMaxを使って、実際に論理回路図を作成してみましょう。無料で利用できるので、公式サイトのリンクからEdrawMaxをダウンロードし、豊富な機能を体験してください。