全加法器電路圖：完整教學

在電子和數位邏輯設計中,加法器是一種對二進位數執行加法運算的數位電路。就電腦而言,加法器用於執行處理器中的算術邏輯單元 (ALU) 任務。在處理器中,它們用於計算地址、遞增或遞減操作、表索引等操作。

來源：www.elprocus.com

它們也用於數字表示,例如二進位編碼的十進位代碼或加3碼。加法器有兩種。

• 半加法器
• 全加法器

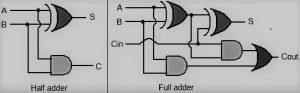
在介紹全加法器之前,有必要了解什麼是半加法器,因為它是全加法器的基礎。

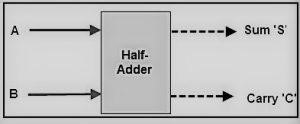
半加法器也是一種用於電子和數位邏輯設計操作的電路。它也用於對二進位數字進行加法運算。在半加法器電路中,我們有兩個單位元的二進位數字0或1,它們是電路的兩個輸入 A 和 B。這些輸入也稱為被加數和加數位元。這些輸入相加,並產生和 S 與進位 C。

可以合併兩個半加法器以形成一個全加法器電路。這是半加法器的簡單定義。現在,讓我們深入探討全加法器。

來源：www.elprocus.com

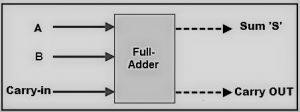
在處理一個或多個位元的二進位數字使用全加法器。它也是一種用於電子和數位邏輯設計的電路,對兩個二進位輸入執行加法運算。全加法器輸入有三個,分別是 A、B 這兩個標準輸入,以及進位C,與半加法器電路不同。

在全加法器中,當第一個加法運算開始時,第一個進位C為零。當從A和B產生的和S時,最後一個有效位的進位將被加到下一個加法運算中,此過程會持續進行直到所有的二進位數字被相加。

全加法器還可以用於8位元、16位元、32位元等二進位數,它是加法器級聯中的組成部分。全加法器通常產生一個兩位元二進位數作為輸出。要對全加法器進行加總,可以用方程式表示。

• S = A ⊕ B ⊕ Cin。
• Cout = (A ⋅ B) + (Cin ⋅ (A ⊕ B))。

來源：www.elprocus.com

只有學習理論是不夠的。我們還必須了解實務面,讓我們的概念變得更加清晰。本節將實際呈現全加法器電路圖、真值表和方程式,並了解製作全加法器的三種方法。

與半加法器相比,全加法器稍微複雜一點,因為全加法器有三個輸入 A、B 和C。通常輸出是C和和S。讓我們從真值表中了解全加法器。

全加法器的真值表

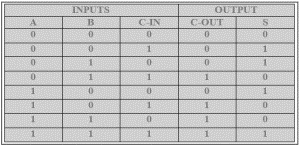
來源：www.elprocus.com

在這裡,我們將其分為輸入運算和輸出結果兩大部分。在輸入部分,我們有A、B和Cin三列。現在在A和B中,以傳統形式放置0和1。首先取A和B的0和1並將它們進行XOR運算。當輸入中1的數量為奇數時,XOR運算結果產生1,否則產生0。

現在取XOR運算後A和B的結果,再次與Cin進行XOR運算。記住,第一個Cin始終為0。在輸出部分,Cout和S是根據三個輸入生成的。如果高(1)的數量為奇數,則產生的高(1)作為0。現在我們來看全加器的電路圖。

全加法器的電路圖

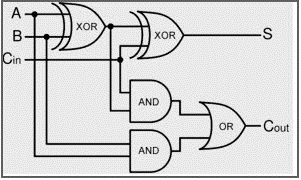
來源：www.elprocus.com

這是一般全加法器的電路圖。在這裡,我們使用了兩個半加法器圖來製作全加法器圖。首先對兩個輸入A和B進行XOR運算,並從它們的結果中對C進行XOR運算。

然後對輸入A和B進行"與"運算,對XOR後的A和B以及Cin也進行"與"運算。兩個與運算的結果進行"或"運算以產生最終的Cout。

因此,從上圖中,我們可以很容易地理解全加法器是組合電路。現在,讓我們看全加法器電路的方程式或表達式。

全加法器方程式或表達式

全加法器的方程式或表達式如下。

• S = a ⊕ b⊕Cin。
• Cout = (a*b) + (Cin*(a⊕b))。

從上面的和S的方程式中,可以很容易地看出,首先將A和B進行XOR運算,然後是Cin。⊕是XOR運算的符號。在Cout表達式中,我們可以看到首先將 A 和 B 進行"與"運算,然後將Cin與A和B的XOR結果進行"與"運算。最後將這些結果進行"或"運算以產生Cout。

從上面的範例在全加法器中,使用了三個邏輯閘,它們是:

• 最重要的XOR閘
• 與閘
• 或閘

我們現在看到和使用的所有電子設備都歸功於加法器。如上所表達,全加法器用於執行邏輯單元運算,這是電腦CPU運算的必要部分。沒有全加法器,我們將無法讓電腦執行任何複雜的工作。全加法器用於對晶片進行編程,這些晶片用於現代汽車、飛機和其他自動化機械中。因此,我們無法忽視生活中的全加法器。

對於這種使用全加法器的複雜電路設計,專家建議使用網路上最好的軟體 EdrawMax。EdrawMax 是一款易於使用的圖表製作軟體,您可以使用它有效率地執行您的任務。

該軟體的開發人員表示,EdrawMax適用於所有人,無論其專業背景如何。該軟體包含各行各業現成的範本和圖庫,您可以使用它們來提高您的生產力。您還可以轉換成不同檔案格式,分享到任何社群媒體網站。該軟體可免費用在您的工作上,但如果您想要更多進階功能,則必須購買該軟體。