Neste artigo
O que é um diagrama de Euler
O diagrama de Euler é a representação da teoria dos conjuntos. Ele ilustra relacionamentos visuais da vida real. Devido à sua semelhança, muitas pessoas ficam confusas entre o diagrama de Euler e o diagrama de Venn. Os diagramas Eulerianos, da mesma forma que os diagramas de Venn, empregam círculos para ilustrar a interação lógica entre os itens.
Apesar de serem componentes da teoria dos conjuntos, o diagrama de Euler apresenta apenas uma parte da relação, ao contrário do diagrama de Venn. Esta relação é aplicável apenas em cenários práticos. No entanto, o diagrama de Venn é aplicável em todas as interações práticas e teóricas possíveis entre conjuntos.
Vamos usar como exemplo duas categorias: um superconjunto de mamíferos e um subconjunto de aves. Mesmo que a área sombreada esteja vazia, um diagrama de Venn indicará a interseção entre os dois conjuntos. Ao contrário, o diagrama de Euler terá apenas dois círculos distintos para mamíferos e aves. É porque eles não estão se cruzando.
A capacidade de visualizar a teoria dos conjuntos torna os diagramas básicos de Venn úteis na educação. Apesar disso, os diagramas de Euler são flexíveis e apresentam elementos estruturais suplementares, como pontos, gráficos e rótulos escritos. Assim, os diagramas de Euler são reconhecidos por sua habilidade em representar hierarquias, auxiliar em tomadas de decisões e analisar perspectivas.
História do Diagrama de Euler
O matemático suíço Leonhard Euler introduziu pela primeira vez os círculos eulerianos no século XVIII. Ele empregou esses diagramas para ilustrar as relações lógicas entre duas categorias. Depois disso, os diagramas de Venn foram reconhecidos no século XIX.
Nos anos 1960, educadores recorreram a esses dois diagramas para aprimorar a compreensão da teoria dos conjuntos. Posteriormente, John Venn, Peirce e Leibniz contribuíram para o aprimoramento dos diagramas de Euler. Hoje, você pode aplicá-los a hierarquias complexas da vida real.
Em um círculo euleriano comum, as categorias são separadas por uma curva ou círculo. Cada curva possui duas zonas, também conhecidas como regiões, interna e externa. Na região interna são ilustrados os elementos do conjunto, enquanto na região externa esses elementos não estão incluídos. O conjunto completo de representações que destaca a interseção de conjuntos é conhecido como diagrama Euleriano.
Diferentemente do diagrama de Venn, conjuntos não sobrepostos não são indicados por espaços vazios sombreados. Em vez disso, separa inteiramente os dois círculos, indicando conjuntos disjuntos.
Exemplo de diagrama de Euler
Tendo definido o conceito de diagrama de Euler, continuemos e observemos alguns exemplos práticos desses diagramas.
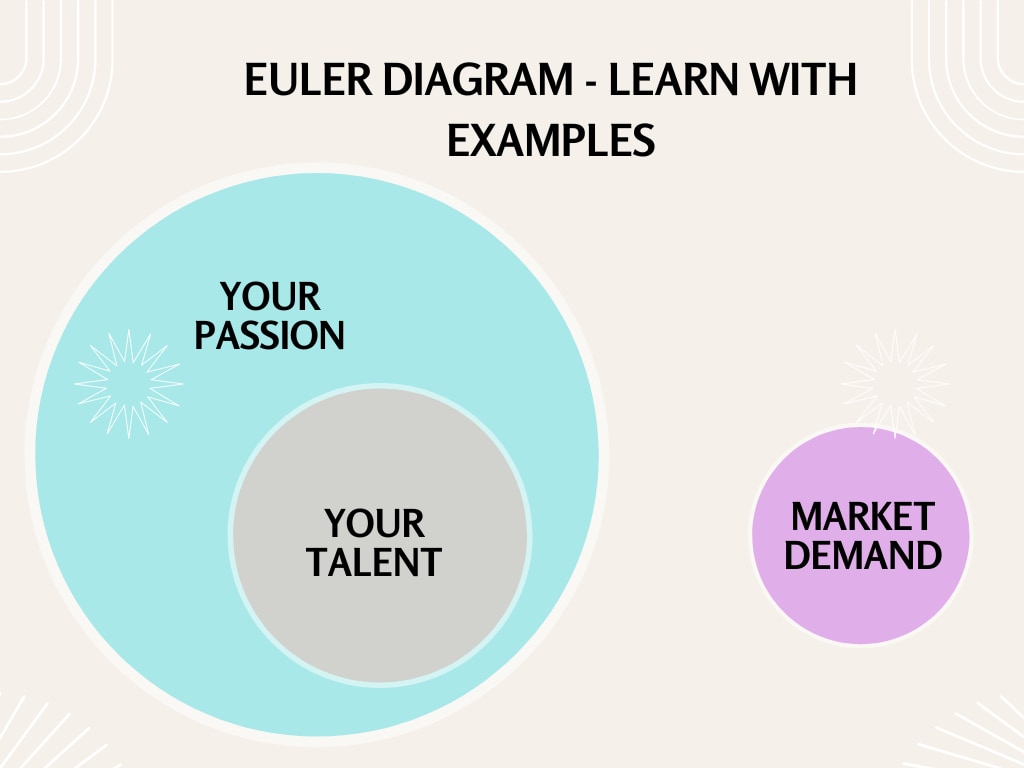
Uma explicação simples para este diagrama de Euler seria: "Todos os sinais de trânsito são objetos estacionários; os carros não estão parados."
A partir desta estrutura hierárquica entre as duas categorias, podemos fazer as seguintes suposições.
- Todos os sinais de trânsito são objetos estacionários. Essa relação é clara ao notar o subconjunto de sinais de trânsito situado dentro do superconjunto de objetos estacionários. É uma visualização de sobreposição em diagramas de Euler.
- Os carros não são objetos estacionários. Neste caso, o subconjunto de carros está fora do superconjunto que engloba objetos estacionários. Trata-se de um exemplo de conjuntos não sobrepostos ou disjuntos, sem qualquer espaço vazio sombreado.
- Nenhum sinal de trânsito é carro, o que significa que essas duas categorias não estão relacionadas. Conseqüentemente, eles estão em círculos diferentes e separados.
Este exemplo apresenta uma relação entre objetos estacionários e veículos em movimento na estrada. A compreensão desse diagrama pode ser útil para qualquer pessoa que tenha planos de dirigir, ajudando a entender o trânsito e a ética rodoviária. Este exemplo também pode ser empregado por educadores para ensinar a turma o vocabulário associado ao trânsito.
Diferença entre o diagrama de Euler e o diagrama de Venn
No âmbito da teoria dos conjuntos, os diagramas de Euler e Venn utilizam abordagens diferentes para ilustrar relações lógicas. Enquanto o diagrama de Venn possui uma área sombreada vazia sobreposta, os diagramas de Euler não apresentam essa característica, tornando-os mais flexíveis e avançados.
Diagrama de Venn vs. Diagramas de Euler
Apesar de suas formas serem semelhantes, ambas são completamente distintas. Aqui estão algumas de suas principais diferenças.
Sobreposição
- Diagrama de Venn - use uma região compartilhada sombreada.
- Diagrama de Euler - as formas são sobrepostas e aninhadas, e pode não existir nenhuma região compartilhada caso não haja sobreposição.
Completude
- Diagrama de Venn - mostra todos os relacionamentos de conjuntos lógicos (pode ser teórico).
- Diagrama de Euler - mostra apenas possíveis relações entre conjuntos (existentes na vida real).
Complexidade
- Diagramas de Venn - são difíceis de ler e compreender, especialmente quando há acima de três categorias.
- Diagramas de Euler - são compreensíveis. Portanto, são ideais para interpretar estruturas e interações de classes complexas.
Expressão
- Diagramas de Venn - possuem alguns relacionamentos definidos, incluindo união, diferença e interseção.
- Diagrama de Euler - oferece uma ilustração de dependências mais amplas entre conjuntos. Portanto, eles são ótimos para mostrar hierarquias complicadas.
Exemplos de diagrama de Euler e diagrama de Venn
Um exemplo é a melhor maneira de dissipar qualquer confusão. Aqui estão exemplos de diagramas de Venn e Euler para esclarecer a confusão:

A relação entre junk food e plantas é ilustrada neste diagrama de Venn. A presença de sobreposição entre alguns elementos sugere que ambos fazem parte da categoria de alimentos comestíveis. No entanto, também ilustra que nem todas as plantas são comestíveis.
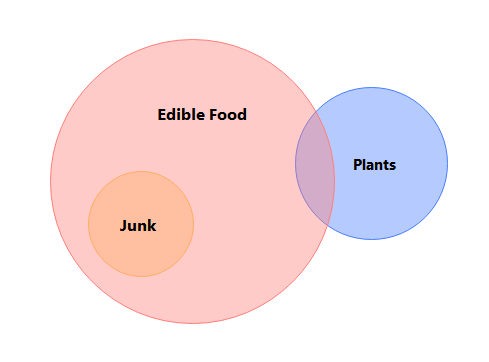
Agora, vejamos a mesma relação, mas num arranjo de Euler. A declaração de uma linha para este exemplo seria: “Todas as porcarias e algumas plantas são alimentos editáveis”.
Aqui estão as seguintes suposições deste exemplo.
- “Toda junk food é comida comestível”. Essa situação ocorre porque os alimentos comestíveis atuam como um superconjunto, enquanto a junk food é um subconjunto. A sobreposição é notável, já que o círculo da junk food está completamente inserido nos alimentos comestíveis.
- “Algumas plantas são alimentos comestíveis”. A sobreposição parcial entre um subconjunto que inclui plantas e alimentos comestíveis é a razão por trás dessa relação. Isso implica que apenas algumas plantas são consideradas boas para o consumo.
- A afirmação "Nenhuma junk food é uma planta" é justificada pelo fato de que ambas têm superconjuntos ou círculos separados no diagrama. Essas duas categorias ilustram uma disjunção neste exemplo.
Como criar um diagrama de Euler
Embora compartilhem semelhanças significativas com os diagramas de Venn, os diagramas de Euler utilizam uma organização diferente. Então, o processo de criação deles é um pouco diferente. Aqui está um guia passo a passo sobre como criar um diagrama de Euler do zero.
É sempre recomendável anotar os dados em papel antes de iniciar. Vamos seguir o processo usando o exemplo a seguir.
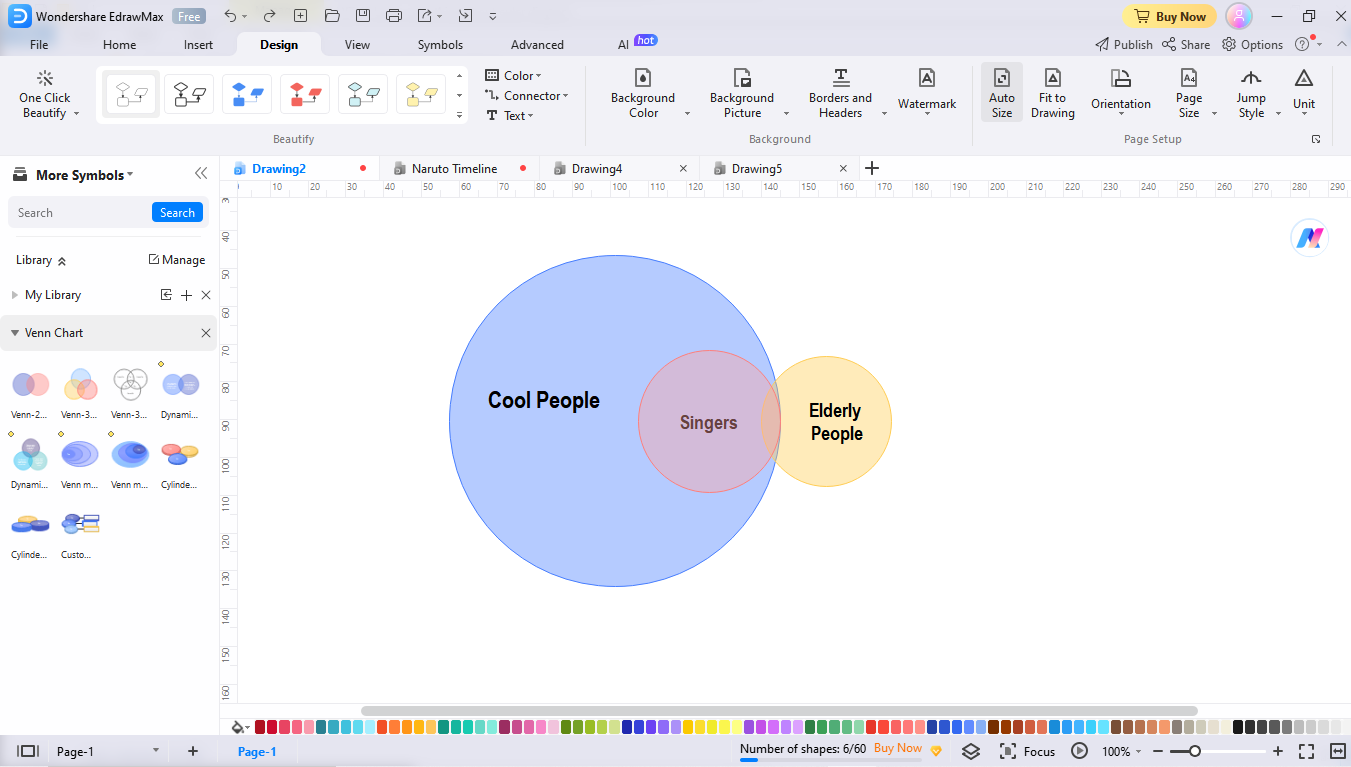
- Afirmação 1: Todos os cantores são pessoas legais.
- Afirmação 2: Alguns idosos são cantores.
- Afirmação 3: Alguns idosos são pessoas legais.
Ao redigir essas declarações, evite pressa, pois elas servirão como guia para o subsequente processo de desenho. A omissão de qualquer uma dessas declarações pode comprometer todo o processo de criação do diagrama.
Passo 1: desenhe três categorias
Abra uma tela online ou pegue uma folha de papel e desenhe três círculos. Independentemente da sua escolha, certifique-se de que seja um material que possa ser apagado, permitindo a adição e remoção de formas em cada etapa. Agora, rotule cada círculo com a categoria necessária. Aqui as rodas serão de cantores, galera e gente bacana. Sobreponha esses três círculos.

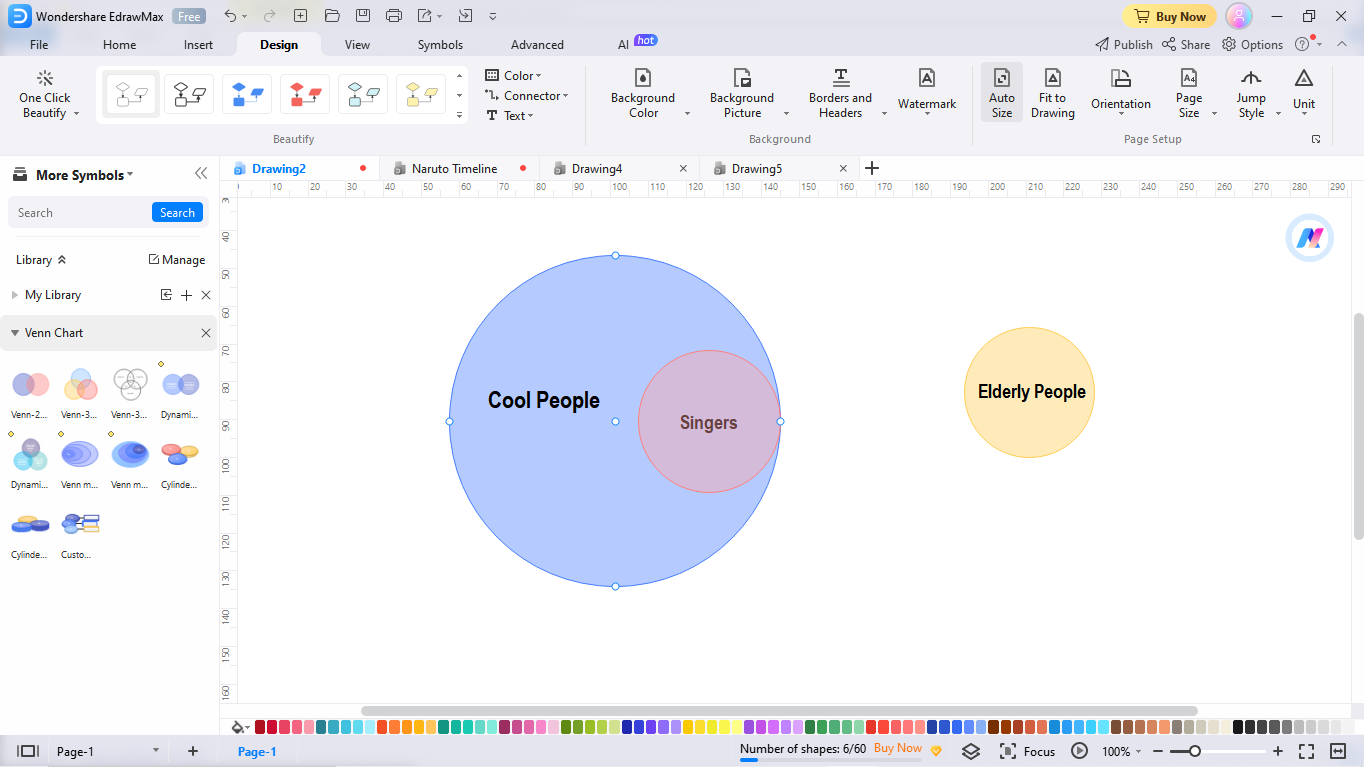
Passo 2: mova os círculos para corresponder à primeira afirmação
Depois disso, volte ao primeiro passo e verifique os dados gravados. Leia a primeira afirmação e mova os círculos correspondentes. Aqui, a primeira afirmação é que “todos os cantores são pessoas legais”. Agora, converta o círculo das pessoas legais em um superconjunto e inclua um subconjunto de cantores nesse círculo anterior.
Passo 3: mova os círculos para corresponder à segunda afirmação
Agora, siga em frente e leia a segunda afirmação: “Alguns idosos são cantores”. Neste ponto, mova o segundo subconjunto que engloba os idosos e sobreponha-o ao subconjunto que contém os cantores.
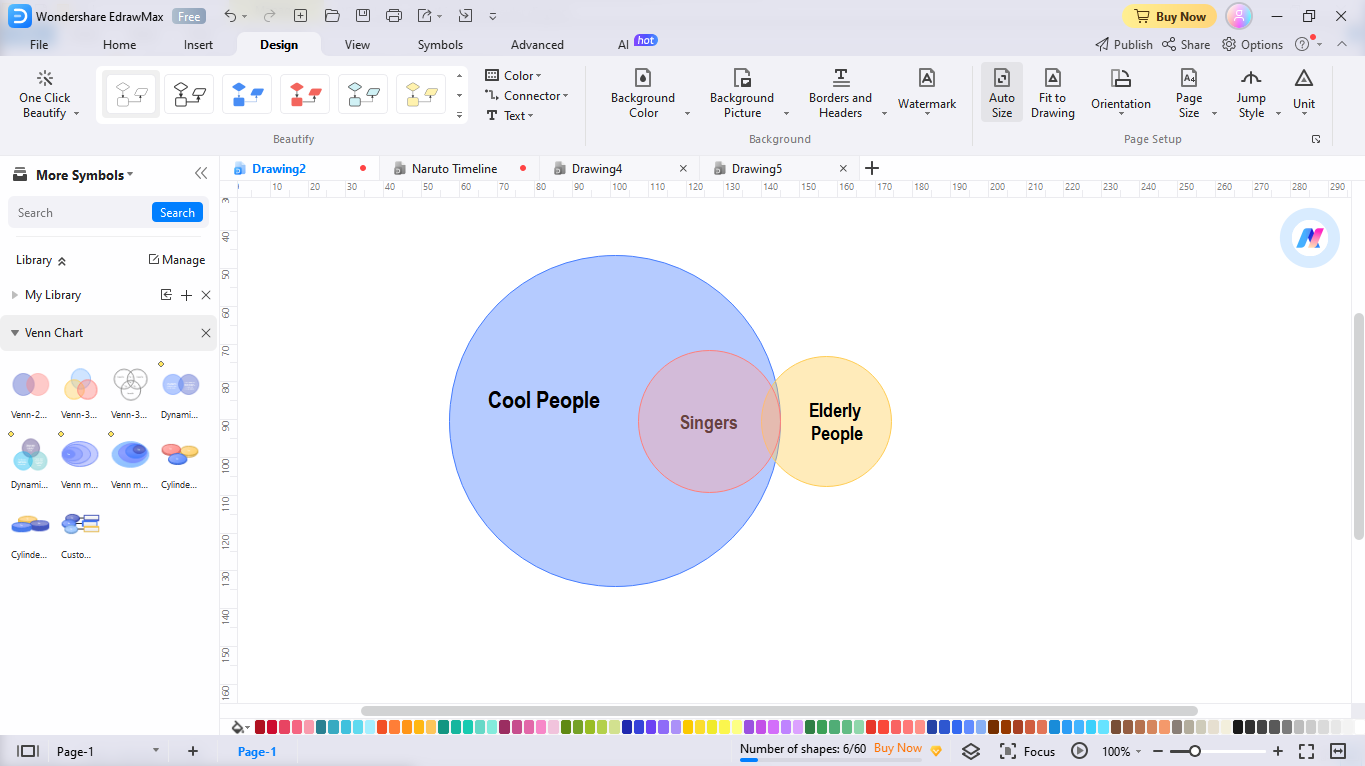
Passo 4: mova os círculos para corresponder à terceira afirmação
Por fim, volte à última afirmação: “Alguns idosos são pessoas legais”. Isso implica que o subconjunto com os idosos deve ser parte de um superconjunto que inclui os cantores. Então, verifique a disposição e ajuste os círculos. Parabéns, seu diagrama de Euler está pronto.
Conclusão
Utilizar diagramas de Euler é uma excelente forma de visualizar várias perspectivas e representar hierarquias complexas. A representação desses diagramas utiliza círculos e curvas fechadas para expressar as interações definidas.
A notável semelhança entre os diagramas de Euler e Venn tende a gerar confusão na maioria das pessoas. Mas não se preocupe se você for um deles. Mesmo com suas semelhanças, os diagramas de Euler apresentam elementos estruturais extravagantes e arranjos flexíveis. É por isso que eles são precisos para situações da vida real.
Então, tudo que você precisa fazer é rastrear essas diferenças. Verifique este guia para diferenciá-los dos diagramas de Venn e reconhecer suas aplicações específicas.


 abaixo.
abaixo. 