Schéma du circuit de l'additionneur complet : Un tutoriel complet

Dans le monde de l'électronique et de la logique numérique, l'additionneur est en fait un circuit numérique utilisé pour effectuer des additions sur des nombres binaires. Les additionneurs sont utilisés pour effectuer la tâche de l'unité logique arithmétique (ULA) dans les processeurs lorsqu'il s'agit d'ordinateurs. Dans les processeurs, ils sont utilisés pour calculer des adresses, des opérations d'incrémentation ou de décrémentation, des indices de table et d'autres opérations.

Source : www.elprocus.com

Ils sont également utilisés pour la représentation des nombres comme le code décimal codé en binaire ou l'excess-3. Il existe deux types d'additionneurs.

• Demi-additionneur
• Additionneur complet

Avant de se lancer dans l'additionneur complet, il est nécessaire de savoir ce qu'est le demi-additionneur car il est la base de l'additionneur complet.

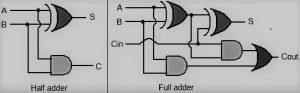
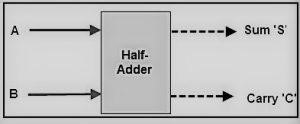
Demi-additionneur est également un circuit utilisé dans les opérations de conception en électronique et en logique numérique. Il est également utilisé pour effectuer des additions sur des nombres binaires. Dans le circuit du demi-additionneur, nous avons deux chiffres binaires d'un seul bit, 0 ou 1, et ce sont les deux entrées A et B du circuit. Ces entrées sont également appelées les bits première opérande et d'addend. Ces entrées sont additionnées, et la somme S avec la retenue C est produite.

Les deux demi-additionneurs peuvent être fusionnés pour former un circuit additionneur complet. C'est la définition simple du demi-additionneur. Maintenant, nous allons nous plonger dans l'additionneur complet.

Source : www.elprocus.com

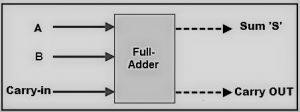
L' additionneur complet est utilisé lorsque vous avez un ou plusieurs nombres binaires d'un bit. C'est également un circuit utilisé en électronique et en conception de logique numérique et il est utilisé pour effectuer une addition sur les deux entrées binaires. Les entrées de l'additionneur complet sont au nombre de trois, et ce sont les entrées A, B, les deux entrées standard, et le Carry C, ce qui le rend différent du circuit du demi-additionneur.

Dans l'additionneur complet, la première retenue C est toujours nulle lorsque la première opération d'addition commence. Lorsque la somme S est générée à partir de A et B, la retenue du dernier bit le moins significatif est ajoutée à l'opération d'addition suivante, et cette tâche est poursuivie jusqu'à ce que tous les nombres binaires soient additionnés.

L'additionneur complet ajoute également des nombres binaires de 8, 16, 32, etc. bits, c'est pourquoi il est le composant de la cascade d'additionneurs. L'additionneur complet produit généralement un nombre binaire de deux bits comme sortie. Si l'on fait le résumé de l'additionneur complet, on peut les représenter dans les équations.

• S = A ⊕ B ⊕ Cin.
• Cout = (A ⋅ B) + (Cin ⋅ (A ⊕ B)).

Source : www.elprocus.com

EdrawMax

Logiciel de diagrammes tout-en-un

Créer plus de 280 types de diagrammes sans effort

Commencez facilement à créer des diagrammes à l'aide de divers modèles et symboles

• Compatibilité supérieure des fichiers : Importer et exporter des dessins vers différents formats de fichiers, tels que Visio
• Prise en charge multiplateforme (Windows, Mac, Linux, Web)

Téléchargement gratuit

Téléchargement gratuit

Téléchargement gratuit

L'étude de la théorie ne suffit pas. Il faut aussi voir les implémentations pratiques pour que nos concepts deviennent plus évidents. Dans cette section, nous allons mettre en pratique le schéma du circuit de l'additionneur complet, la table de vérité et l'équation. Et connaîtra le processus de fabrication d'un additionneur complet de trois façons.

L'additionneur complet est un peu plus complexe à mettre en œuvre que le demi-additionneur car l'additionneur complet a trois entrées A, B et C. Habituellement, la sortie est C et la somme S. Comprenons l'additionneur complet à partir de sa table de vérité.

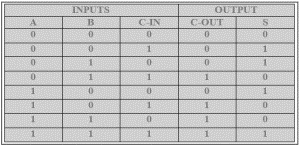
Table de vérité de l'additionneur complet

Source : www.elprocus.com

Donc, ici nous avons deux grandes sections pour les opérations d'entrée et les résultats de sortie. Dans la section d'entrée, nous avons trois colonnes pour A, B, et Cin. Maintenant dans A et B, mettez les 0 et les 1 sous la forme traditionnelle. D'abord, prenez les 0 et les 1 de A et B et faites un XOR entre eux. Lorsque le nombre de 1 en entrée est impair dans l'opération XOR, le 1 est produit dans le résultat, sinon 0.

Maintenant, prenez les résultats XOR de A et B et XORez-les à nouveau avec Cin. Rappelez-vous que le premier Cin est toujours 0. Dans la section de sortie, Cout et S sont générés en voyant les trois entrées. Si les highs(1) sont impairs, alors le high(1) est produit comme 0. Maintenant, nous allons voir le schéma du circuit de l'additionneur complet.

Schéma du circuit de l'additionneur complet

Source : www.elprocus.com

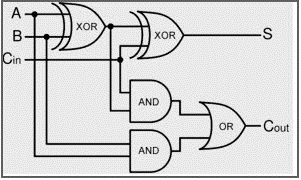
Voici la représentation du schéma général du circuit de l'additionneur complet. Ici, nous avons utilisé deux diagrammes de demi-addition pour réaliser le diagramme de l'additionneur complet. Les deux entrées A et B sont d'abord combinées par XOR, et à partir de leur résultat, le C est également combiné par XOR.

Les entrées A et B sont ensuite AND, puis XOR A et B et Cin sont également AND ensemble. Les deux résultats de l'ET sont combinés par Ored pour produire le Cout final.

Ainsi, à partir du schéma ci-dessus, nous pouvons facilement comprendre que l'additionneur complet est un circuit combinatoire. Maintenant, voyons l'équation ou l'expression du circuit de l'additionneur complet.

Equation ou expression de l'additionneur complet

L'équation ou l'expression de l'additionneur complet est are, et ils sont les suivants.

• S = a ⊕ b⊕Cin.
• Cout = (a*b) + (Cin*(a⊕b)).

D'après l'équation de la somme S ci-dessus, il est facilement visible que l'on effectue d'abord une opération XOR sur A et B, puis sur Cin. ⊕ est le symbole de l'opération XOR. Dans l'expression Cout, nous pouvons voir que A et B sont d'abord combinés par ET, puis que Cin est combiné par ET avec le XOR de A et B. Ensuite, ces résultats sont combinés par OU pour produire l'équation Cout.

Donc, à partir du travail ci-dessus, nous pouvons dire que dans l'additionneur complet, trois portes logiques sont utilisées, et elles sont.

• La porte XOR, la plus importante
• Porte ET
• Porte OU

Les machines électroniques utiles que nous voyons et utilisons aujourd'hui sont grâce à l'additionneur. Comme nous l'avons vu ci-dessus, l'additionneur complet est utilisé pour effectuer les opérations de l'unité arithmétique et logique, une partie nécessaire des opérations de l'unité centrale de l'ordinateur. Sans cela, nous ne serons pas en mesure d'effectuer les travaux complexes que les ordinateurs réalisent aujourd'hui. Les additionneurs complets sont utilisés pour programmer les puces, et ces puces sont utilisées dans les véhicules modernes, les avions et autres machines automatiques. Nous ne pouvons donc pas ignorer l'additionneur complet dans notre vie.

Pour cette conception complexe de circuits utilisant des additionneurs complets, les experts recommandent d'utiliser le meilleur logiciel sur Internet, EdrawMax. EdrawMax est un logiciel de création de diagrammes facile à utiliser que vous pouvez utiliser pour effectuer votre tâche efficacement.

Les développeurs du logiciel affirment que le logiciel s'adresse à tout le monde, quel que soit son parcours professionnel. Le logiciel contient tous les modèles pré-générés essentiels et les bibliothèques que vous utilisez pour booster votre production. Vous pouvez également télécharger votre résultat dans différents formats et le partager sur n'importe quel site de médias sociaux. Le logiciel est gratuit pour votre travail primaire, mais vous devez l'acheter si vous souhaitez des fonctionnalités plus avancées.