En este artículo
Qué es un diagrama de Euler
El diagrama de Euler es la representación con que se conoce la teoría de conjuntos. Sirve para ilustrar la relación visual entre conjuntos del mundo real. La mayor parte de la gente lo confunde con el diagrama de Venn debido a su parecido. Al igual que los diagramas de Venn, los diagramas de Euler utilizan círculos para representar la interacción lógica entre elementos.
Aunque ambos diagramas forman parte de la teoría de conjuntos, el diagrama de Euler sólo muestra una parte de dicha interrelación. Tal interrelación sólo se aplica en situaciones prácticas. Sin embargo, el diagrama de Venn se aplica en todas las posibles interacciones prácticas y teóricas entre conjuntos.
Por ejemplo, pongamos como ejemplo dos categorías: un subconjunto de mamíferos y un subconjunto de aves. Un diagrama de Venn mostrará la intersección entre los dos conjuntos, aunque el área sombreada esté vacía. En cambio, el diagrama de Euler sólo tendrá dos círculos separados para mamíferos y aves. Por ello, no se intersectan.
Los diagramas de Venn básicos permiten visualizar la teoría de conjuntos, lo que los hace aptos para el ámbito educativo. Sin embargo, los diagramas de Euler son flexibles y tienen elementos estructurales adicionales como puntos, gráficos y etiquetas inscritas. Por lo tanto, los diagramas de Euler son más conocidos para representar jerarquías, toma de decisiones y análisis de perspectivas.
Historia del diagrama de Euler
El matemático suizo Leonhard Euler introdujo por primera vez los "círculos de Euler" en el siglo XVIII. Utilizó estos diagramas para representar las relaciones lógicas entre dos categorías. Posteriormente, en el siglo XIX se reconocieron los diagramas de Venn.
En la década de 1960, los educadores utilizaron estos dos diagramas para profundizar en la enseñanza de la teoría de conjuntos. Más tarde, John Venn, Peirce y Leibniz contribuyeron al desarrollo de los diagramas de Euler. Hoy en día, puedes aplicarlos al estudio de jerarquías complejas en la vida real.
El típico círculo de Eluer separa categorías delimitadas por una curva o círculo. Cada curva tiene dos áreas, también conocidas como regiones, una interna y otra externa. La región interna ilustra los elementos del conjunto, mientras que la región externa no forma parte del conjunto. Todo este esquema que representa la intersección de conjuntos se denomina diagrama de Euler.
A diferencia del diagrama de Venn, los conjuntos que no se superponen en este caso no se muestran a través de espacios vacíos sombreados. En cambio, se separan completamente los dos círculos y se representan como conjuntos disjuntos.
Ejemplo de diagrama de Euler
Ahora que hemos definido el concepto de diagrama de Euler, veamos algunos ejemplos del mismo.
a continuación. 
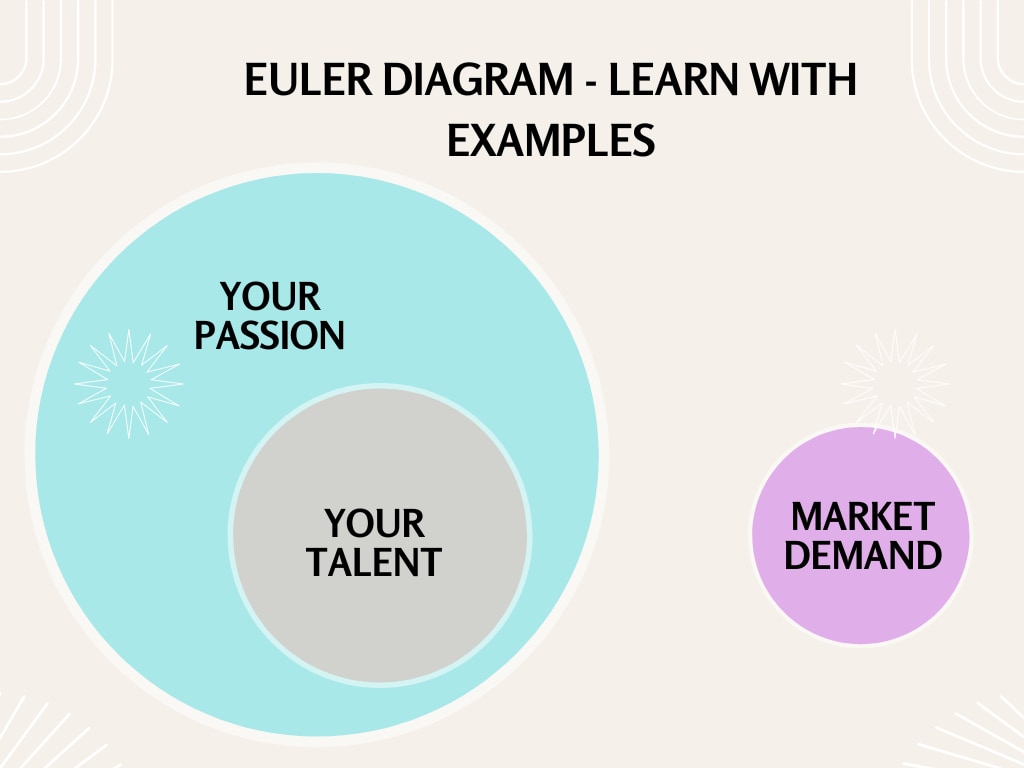
Una frase para describir este diagrama de Euler sería: "Todas las señales de tráfico son objetos inmóviles, pero los autos no lo son".
A partir de esta estructura jerárquica de ambas categorías, podemos hacer las siguientes suposiciones.
- Todas las señales de tráfico son objetos inmóviles. Se puede ver a través del subconjunto de señales de tráfico presente dentro del superconjunto de objetos inmóviles. Es una visualización de la superposición en los diagramas de Euler.
- Los autos no son objetos fijos. Se trata de un subconjunto de autos que se encuentra fuera del superconjunto de objetos fijos. Es un ejemplo de conjuntos no superpuestos o disjuntos sin espacios vacíos sombreados.
- No hay señales de tráfico que sean autos, lo que significa que estas dos categorías no están relacionadas. Por lo tanto, están en diferentes conjuntos disjuntos.
Este ejemplo representa una relación entre objetos inmóviles y vehículos en movimiento en la carretera. Es una buena forma de entender el tráfico y la ética vial para cualquier persona que quiera conducir. Además, los educadores pueden utilizar este ejemplo para informar a la clase sobre lo que se conoce como "vocabulario vial".
Diferencia entre el diagrama de Euler y el diagrama de Venn
Al pertenecer a la teoría de conjuntos, los diagramas de Euler y Venn utilizan diferentes perspectivas para definir relaciones lógicas. El diagrama de Venn tiene un área sombreada vacía que se superpone, mientras que los diagramas de Euler no tienen tal área, lo que los hace más variables y desarrollados.
Diagrama de Venn Vs. Diagramas de Euler
Aunque sus formas son parecidas, ambos son completamente diferentes. A continuación te mostramos algunas de sus principales diferencias.
Superposición
- Diagrama de Venn - utiliza una región que aparece sombreada y que se está usando para unir dos conjuntos.
- Diagrama de Euler - utiliza formas superpuestas y anidadas; puede no tener ninguna región que se use para unir conjuntos.
Funcionalidad
- Diagrama de Venn - muestra todas las relaciones lógicas del conjunto (puede ser teórico).
- Diagrama de Euler - sólo muestra las posibles relaciones entre conjuntos ( las que existen en la vida real).
Complejidad
- Diagramas de Venn - son difíciles de leer y comprender, sobre todo cuando hay más de tres categorías.
- Diagramas de Euler - son fáciles de interpretar. Por lo tanto, son adecuados para representar estructuras de clases e interacciones complejas.
Expresión
- Diagramas de Venn - se dan algunas relaciones de conjunto, como la unión, la diferencia y la intersección.
- Diagrama de Euler - muestra interacciones más extensas entre conjuntos. Por lo tanto, son ideales para representar jerarquías complejas.
Ejemplos de diagramas de Euler y de Venn
Para disipar cualquier duda, mejor un ejemplo. A continuación te ofrecemos algunos ejemplos de diagramas de Venn y de Euler que te ayudarán a comprender mejor los conceptos:
El diagrama de Venn que figura aquí ilustra la relación entre la comida chatarra y las plantas. Hay una superposición de algunos elementos, lo que sugiere que ambos pertenecen a la categoría de alimentos que se pueden consumir. Sin embargo, también ilustra que no todas las plantas son comestibles.
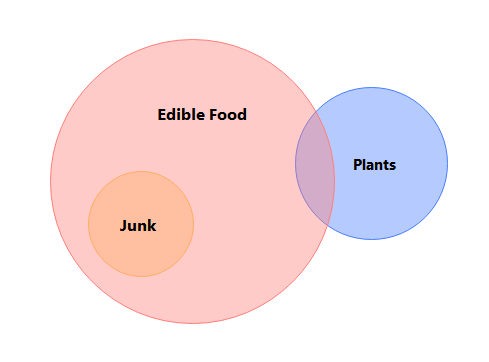
Ahora, veamos la misma relación pero en una distribución de Euler. El enunciado en una línea para este ejemplo sería: "Toda la comida chatarra y algunas plantas son alimentos que se pueden consumir."
Revisemos las siguientes suposiciones de este ejemplo.
- "Toda la comida chatarra pertenece a la categoría de alimentos que se pueden consumir". Esto se debe a que los alimentos que se pueden consumir son un superconjunto, y la comida chatarra es un subconjunto. En el conjunto de la comida chatarra se encuentran los alimentos que se pueden consumir, lo que muestra una gran superposición entre las dos categorías.
- "Algunas plantas son alimentos aptos para el consumo". Esto se debe a que un subconjunto formado por plantas se superpone en parte con los alimentos aptos para el consumo. Sugiere que sólo algunas plantas son buenas para comer.
- "Ninguna comida chatarra es también una planta", ya que tanto la comida chatarra como las plantas tienen superconjuntos o conjuntos separados en el diagrama. En este ejemplo, estas dos categorías representan una disyunción.
Cómo crear un diagrama de Euler
A pesar de su gran parecido con el diagrama de Venn, los diagramas de Euler utilizan una distribución diferente. Por lo tanto, su proceso de creación es un poco distinto. A continuación te presentamos una guía detallada sobre cómo crear un diagrama de Euler desde cero.
Antes de empezar, siempre es mejor anotar los datos en una hoja aparte. Sigue dicho proceso con el siguiente ejemplo.
- Afirmación 1: Todos los cantantes son geniales.
- Afirmación 2: Algunas personas mayores son cantantes.
- Afirmación 3: Algunas personas mayores son geniales.
Tómate tu tiempo para escribir estas afirmaciones, ya que te serán de ayuda en el proceso de dibujo. Omitir alguna de estas afirmaciones puede afectar a todo el proceso de creación del diagrama.
100% Seguro | Sin anuncios |
Impulsado por IA
Calificación G2: 4,5/5 (Más de 2360 reseñas)
100% Seguro | Sin anuncios | Impulsado por IA
Calificación G2: 4,5/5 (Más de 2360 reseñas)
100% Seguro | Sin anuncios | Impulsado por IA
Calificación G2: 4,5/5 (Más de 2360 reseñas)
Paso 1: Traza tres categorías
Ve a un lienzo en línea o coge una hoja de papel y dibuja tres círculos. Sea cual elijas, asegúrate de que se puede borrar para que puedas añadir y quitar formas según vayas avanzando. Ahora, etiqueta cada círculo con la categoría que corresponda. En este caso, los conjuntos serán cantantes, chicos y personas geniales. Une estos tres círculos.
Paso 2: Desplaza los círculos para que coincidan con el primer enunciado
Después de esto, vuelve al primer paso y verifica los datos que has anotado. Lee la primera afirmación y mueve los círculos correspondientes. En este caso, la primera afirmación es que "todos los cantantes son geniales". Por lo tanto, cambia el conjunto de las "personas geniales" por un superconjunto y coloca un subconjunto formado por cantantes en el círculo anterior.
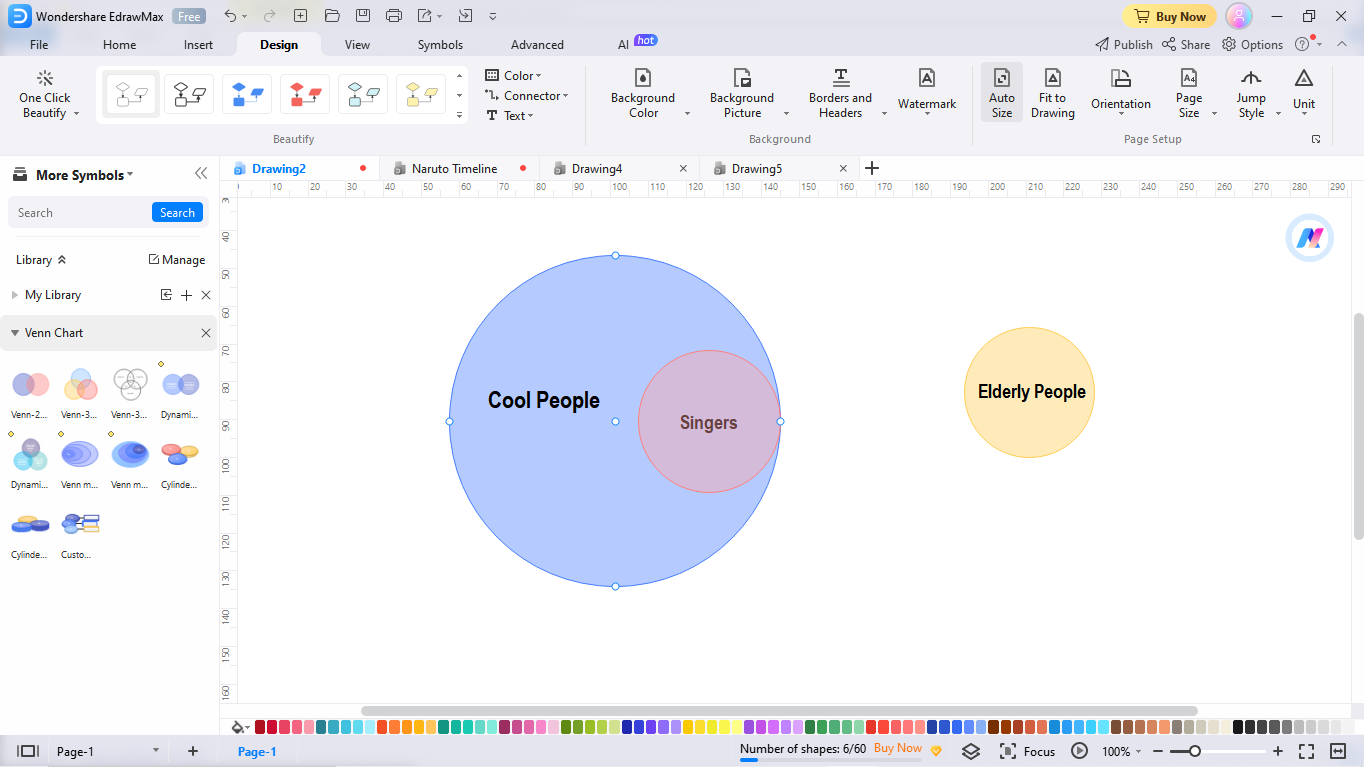
Paso 3: Mover los círculos para que coincidan con la segunda afirmación
Ahora, sigue avanzando y lee la segunda afirmación, "Algunas personas mayores son cantantes". Luego, desplaza el segundo subconjunto que contiene a las personas mayores y colócalo sobre el subconjunto que contiene a los cantantes.
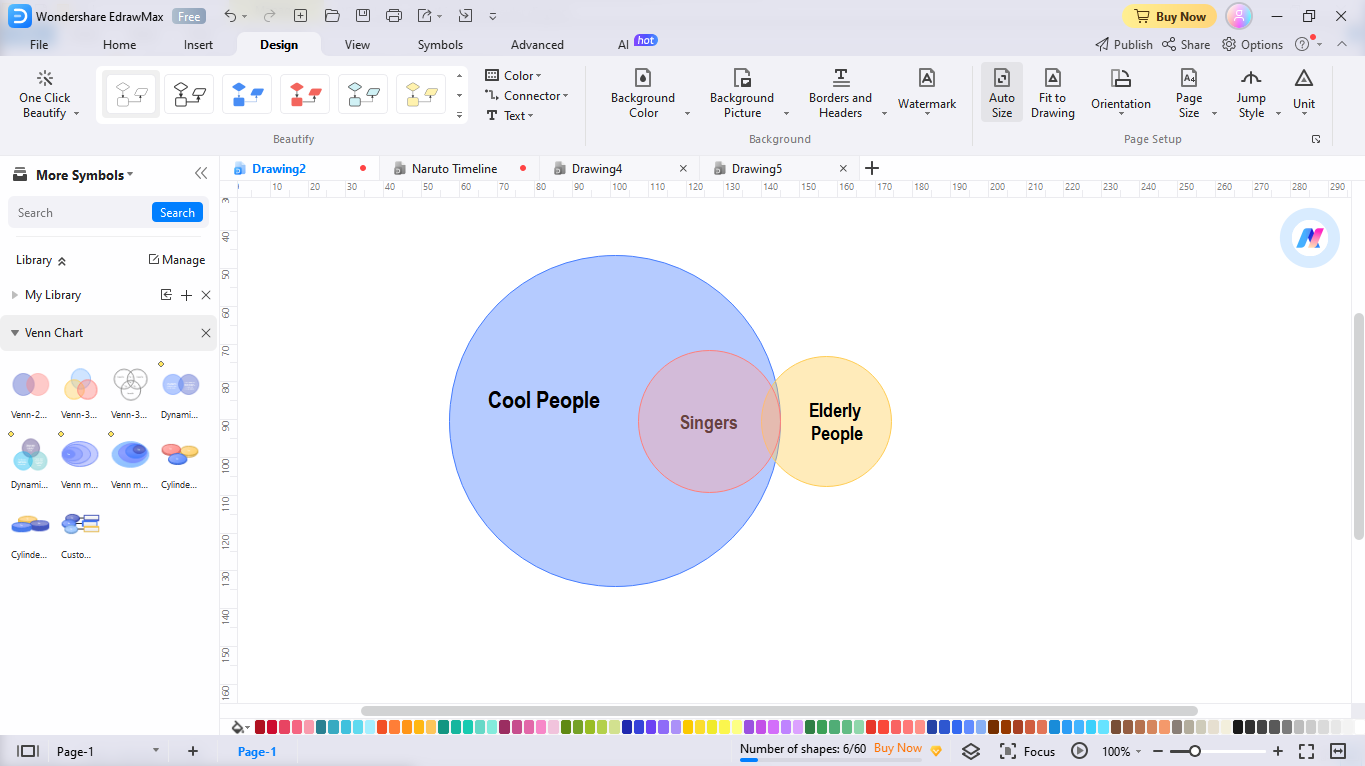
Paso 4: Mover los círculos para que coincidan con la tercera afirmación
Por último, vuelve a la última afirmación, "Algunas personas mayores son geniales". Significa que el subconjunto que contiene a las personas mayores debe estar presente en un superconjunto que contenga cantantes. Por tanto, verifica la distribución y ajusta los conjuntos. ¡Felicidades, tu diagrama de Euler está listo!
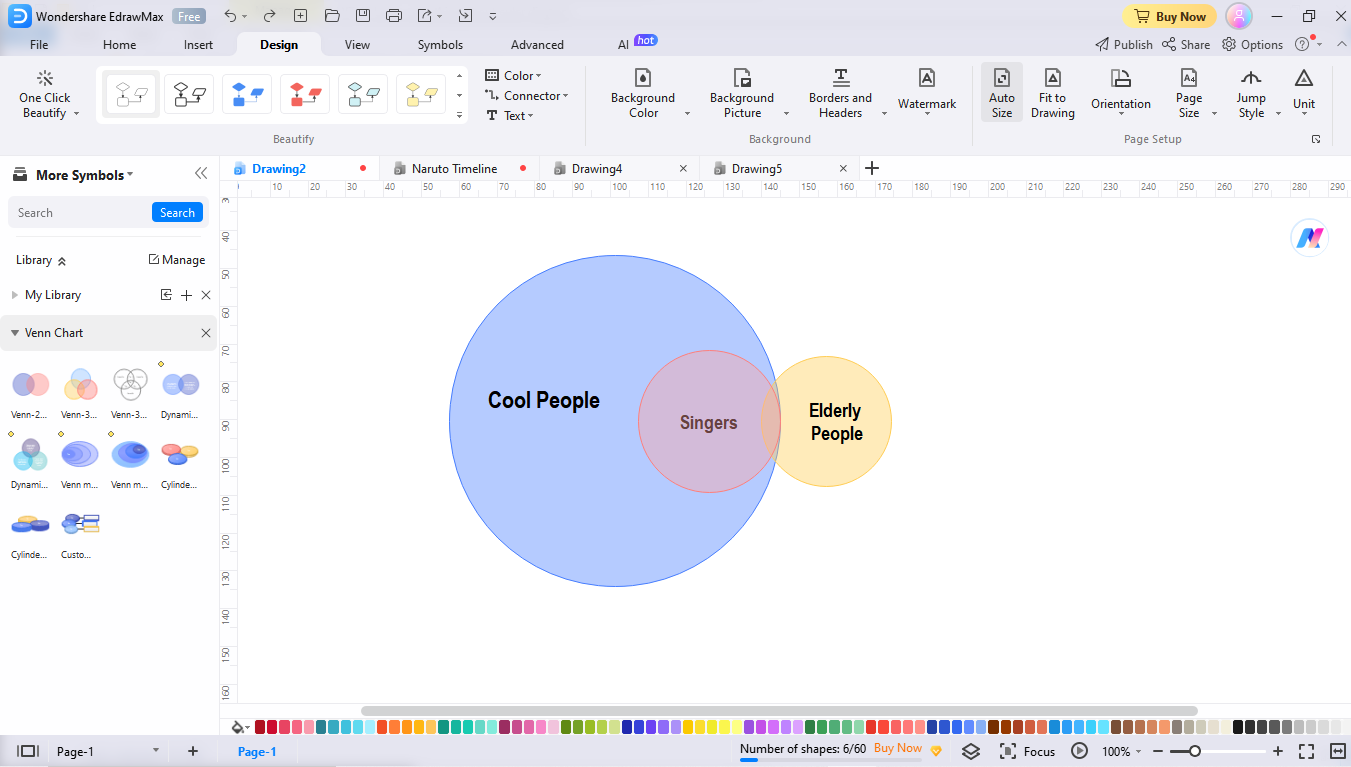
Conclusión
Los diagramas de Euler son excelentes para visualizar distintas perspectivas y representar jerarquías complejas. En estos diagramas se utilizan círculos y curvas cerradas para representar las interacciones de los conjuntos.
La semejanza sorprendente que hay entre los diagramas de Euler y los de Venn confunde a la mayoría de las personas. Pero no te preocupes si eres una de ellas. A pesar de sus similitudes, los diagramas de Euler cuentan con elementos estructurales muy elaborados y una organización bastante adaptable. Por eso son tan precisos en situaciones de la vida real.
Así que lo único que necesitas es detectar estas diferencias. Echa un vistazo a esta guía para saber diferenciarlos de los diagramas de Venn e identificar cuál sería lo más adecuado en cada caso.
EdrawMax EscritorioEdrawMax AppEdrawMax Online
